In un articolo precedente abbiamo introdotto il concetto di Machine learning e come l’apprendimento statistico possa identificare automaticamente delle strutture nei dati e quindi effettuare predizioni con elevata accuratezza. In questo articolo, usando dei dati che riportano specifiche informazioni, creeremo un modello di machine learning.
Oltre ad essere un elemento così importante per la sopravvivenza degli esseri umani, gli alberi hanno anche ispirato un’ampia varietà di algoritmi nel Machine Learning sia per la classificazione che per la regressione. Gli alberi decisionali, come suggerisce il nome, sono alberi di decisioni.
Cos’è un albero decisionale
Di solito si parte da una domanda che si biforca in due o più rami. Sarebbe possibile ottenere più di due rami ma per il momento non complichiamoci la vita (quindi useremo una risposta binaria: si o no)… Gli alberi in informatica sono strani, perché invece di crescere verso l’alto, crescono verso il basso: in pratica dobbiamo capovolgere l’albero. L’elemento che sta in cima si chiama radice (root) ed è il punto da dove parte tutto. I rami sono i segmenti che collegano la radice a nodi interni o alle foglie; queste ultime rappresentano le “decisioni”.
Gli alberi sono importanti in quanto ci permettono di visualizzare graficamente un algoritmo, ma anche il funzionamento dell’apprendimento automatico. Prendiamo questo algoritmo come esempio (rif. www.wikiwand.com/en/Decision_tree_learning).
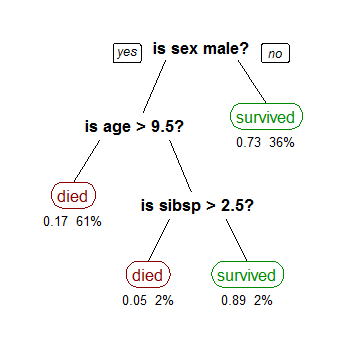
Questo algoritmo prevede la probabilità che un passeggero sopravviva sul Titanic. “Sibsp” è il numero di coniugi o fratelli a bordo della nave. I numeri sotto le foglie mostrano la probabilità di sopravvivenza e la percentuale di osservazioni nella foglia. Riassumendo: le possibilità di sopravvivenza erano buone se tu fossi (1) una femmina o (2) un maschio di età inferiore ai 9,5 anni con meno di 2,5 fratelli.
Questo tipo di albero è un albero di classificazione perché le foglie possono assumere un insieme discreto di valori. In breve: vogliamo classificare ogni persona sulla nave come più probabile che muoia o sopravvissuta.
Come si costruisce?
Esistono diversi algoritmi per costruire un albero. Uno degli algoritmi storici è l’ID3, Iterative Dichotomiser 3. L’albero è costruito in maniera top-down usando una politica nota come divide et impera.
ID3 (Examples, Target_Attribute, Attributes)
Create a root node for the tree
If all examples are positive, Return the single-node tree Root, with label = +.
If all examples are negative, Return the single-node tree Root, with label = -.
If Atributes list is empty, then Return the single node tree Root, with label = most common value of the target attribute in the examples.
Otherwise Begin
A ← The Attribute that best classifies examples.
Decision Tree attribute for Root = A.
For each possible value, vi, of A,
Add a new tree branch below Root, corresponding to the test A = vi.
Let Examples(vi) be the subset of examples that have the value vi for A
If Examples(vi) is empty
Then below this new branch add a leaf node with label = most common target value in the examples
Else below this new branch add the subtree ID3 (Examples(vi), Target_Attribute, Attributes – {A})
End
Return RootSubito dopo l’inizio del ciclo (for each), l’algoritmo deve scegliere l’attributo che meglio classifica gli esempi. Come lo farà? Quale attributo dovremmo selezionare per costruire l’albero decisionale più corretto e preciso? Uno dei metodi comunemente usati per capire qual è l’attributo migliore è l’information gain. Viene calcolato utilizzando un’altro valore chiamato entropia.
Entropia
L’entropia è un concetto usato in fisica e matematica che si riferisce alla casualità o all’impurità di un sistema. Shannon estese il concetto di entropia termodinamica nel 1948, lo introdusse in studi statistici e suggerì la seguente formula per l’entropia statistica: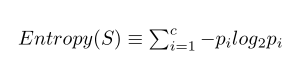 
La formula è una sommatoria dove l’esponente c è il numero di classi o attributi (nel nostro caso il numero di colori è 2) e l’elemento pi è il rapporto tra il valore della classe i-esima e la somma totale del valore delle classi.
Esempio: hai 2 sacchetti pieni di cioccolatini. I cioccolatini possono essere rossi o blu. Decidi di misurare l’entropia dei sacchetti contando il numero di cioccolatini. Quindi ti siedi e inizi a contare. Dopo 2 minuti, scopri che la prima borsa contiene 50 cioccolatini, 25 di colore rosso e 25 di colore blu. La seconda borsa ha anche 50 cioccolatini, ma tutti blu.
Nel primo caso, il valore di pi è uguale a 25 diviso 50 sia per rosso che per blu, perché i cioccolati di numero pari. Quindi la formula sarà la seguente:
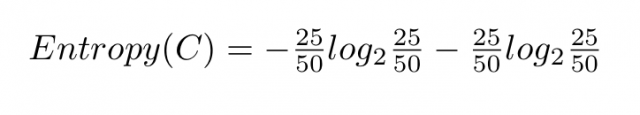
il cui risultato è uguale a 1. Quindi, il primo sacchetto ha entropia 1 poiché i cioccolatini sono equamente distribuiti. Nel secondo caso è facilmente verificabile che l’entropia è uguale a zero perché non c’è casualità. In altre parole, l’entropia sarà massima nel nostro set di dati se i risultati hanno la stessa probabilità di accadimento.
Information Gain
L’information gain è il grado di informazione associato ad ogni attributo.
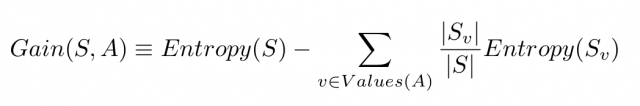
S si riferisce all’intero insieme di esempi che abbiamo. A è l’attributo che vogliamo dividere . | S | è il numero di esempi e | Sv | è il numero di esempi per il valore corrente dell’attributo A.
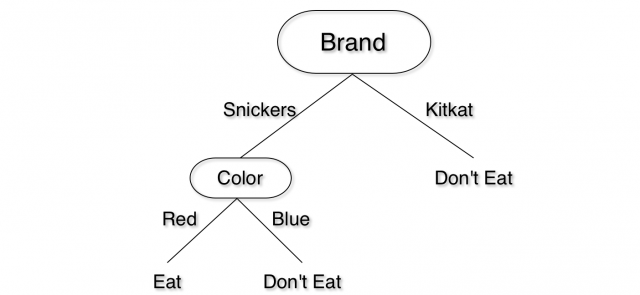
Prendiamo il nostro esempio di cioccolatini e aggiungiamo qualche attributo in più. Sappiamo già che la scatola 1 ha 25 cioccolatini rossi e 25 blu. Prenderemo in considerazione anche la marca di cioccolatini. Tra quelli rossi, 15 sono Snickers e 10 sono Kit Kats. In quelli blu, 20 sono Kit Kats e 5 sono Snickers. Se consideriamo l’attributo colore ne abbiamo 25 rossi e 25 blu. Se consideriamo il marchio attributo, abbiamo 20 Snickers e 30 Kit Kats. Supponiamo di voler mangiare solo Snickers rossi. Allora i 15 cioccolatini Snickers rossi diventano esempi positivi mentre tutto il resto (cioè i rimanenti 35), quali ad esempio Snickers blu e Kit Kats rossi sono esempi negativi.
L’entropia del set di dati rispetto alle nostre classi (mangiare / non mangiare) è:
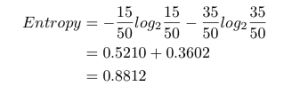
Per costruire l’albero, dobbiamo selezionare uno dei due attributi (colore o marca) per il nodo radice. Vogliamo scegliere l’attributo con il più alto guadagno di informazioni. L’information gain rispetto al colore sarebbe:
L’entropia dei cioccolatini rispetto alla classe è 0,8812. Per l’entropia dei cioccolatini rossi, vogliamo mangiare 15 Snickers ma non 10 Kit Kats. L’entropia dei cioccolatini rossi è:
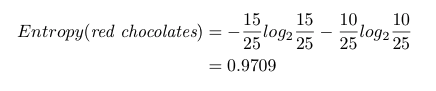
Per i cioccolatini blu, non vogliamo assolutamente mangiarli. Quindi l’entropia è 0.
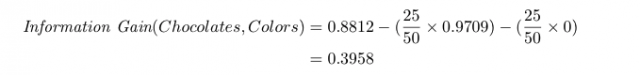
L’information gain rispetto al colore è quindi 0.3958:
Diamo adesso un’occhiata al marchio. Vogliamo mangiare 15 Snickers su 20. Non vogliamo mangiare nessun Kit Kats. L’entropia di Snickers è
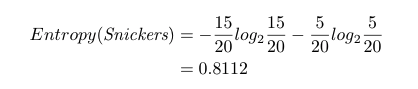
Non vogliamo mangiare Kit Kats, quindi l’entropia è 0. L’information gain sarà:
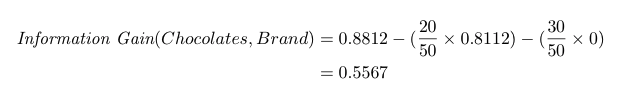
Il nostro information gain rispetto alla marca è 0,5567.
Da momento che l’information gain rispetto alla marca è maggiore, allora la radice dell’albero decisionale partirà dal marchio. Per il livello successivo, rimane solo l’attributo colore. Possiamo facilmente dividere in base al colore senza dover fare calcoli. Il nostro albero decisionale avrà questo aspetto:
