Vai al contenuto

La Notazione O Grande

Comprendere la notazione O-grande è piuttosto importante quando si crea un algoritmo per un progetto che utilizza un set di dati archiviato da qualche parte su un server. Per progetti semplici è piuttosto semplice affrontare un problema: solitamente non ci si preoccupa della complessità del tempo e si fa affidamento alla potenza di calcolo del server hosting. Chi se ne frega se utilizziamo doppi cicli e tripli cicli… Alla fine stiamo operando su un set di dati piccolo, non più di un migliaio di righe: il tempo di elaborazione sarà pressoché istantaneo.  Ma cosa succede se questi dati aumentano e proviamo a interrogare un set di dati nell’ordine delle 100.000 righe?

Purtroppo, all’aumentare della dimensione dell’input (nel nostro caso il set di dati) aumenta il tempo necessario al completamento dell’esecuzione dell’algoritmo,. La variazione può essere anche molto significativa.

I classici esempi accademici su cui si calcola la complessità in notazione O-grande sono gli algoritmi di ordinamento dei numeri. E’ chiaro che l’efficienza di un algoritmo deve essere considerata partendo con un set di dati elevato (diciamo da 100.000 numeri in su), altrimenti le prestazioni di qualsiasi algoritmo, che sia ben o mal progettato, saranno impercettibili se confrontate con altri algoritmi.

Ma come si fa a calcolare quanto tempo e quante risorse vengono impiegate durante l’esecuzione di un algoritmo? Per studiarne la complessità, ci viene in aiuto appunto la notazione O-grande.

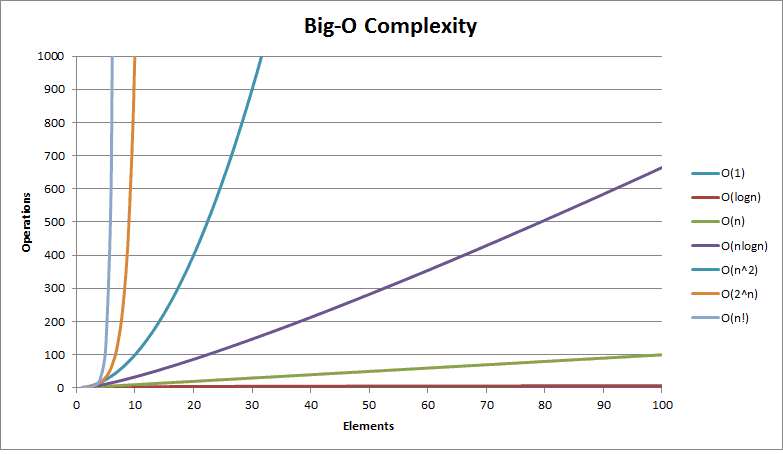
Nell’analisi degli algoritmi si utilizzano solitamente le seguenti classi di funzioni (in ordine crescente di grandezza):

  • Funzione costante: O(1)
  • Funzione logaritmica: O(log(n))
  • Funzione lineare: O(n)
  • Funzione loglineare: O(n log(n))
  • Funzione quadratica: O(n²)
  • Funzione polinomiale: O(nc)
  • Funzione esponenziale: O(cn)
  • Funzione fattoriale: O(n!)

O(1)

O(1) è la complessità costante nel tempo. Ciò significa che un algoritmo di ordine O(1) impiegherà sempre la stessa quantità di tempo a prescindere da quanto grande sia il set di dati che viene dato in pasto all’algoritmo. Un esempio comune è l’accesso a un elemento di un array tramite il suo indice. Solitamente nel calcolo della complessità, tali valori non vengono considerati.

var arr = [1,2,3,4,5];
arr[2]; // => 3

O(N)

La complessità O(N) è la complessità lineare, cioè quando il tempo di esecuzione è direttamente proporzionale dalle dimensioni del set di dati in input. L’esempio classico è quello relativo all’attraversamento di un array o di una lista, che avviene solitamente mediante un ciclo For o While. In tal caso, attraversare un array di un milione di elementi non è la stessa cosa che attraversare un array di 1000 elementi.

O(N²)

Il vero cruccio di ogni informatico è quello di evitare questa complessità. La più odiata da tutti poiché corrisponde alla complessità quadratica, cioè quando il tempo di esecuzione è proporzionale al quadrato della dimensione dell’input. Quindi se l’algoritmo avesse come input un array di 2 elementi, il tempo di esecuzione sarebbe di 4 unità; se l’array fosse di 4 elementi, l’algoritmo avrebbe un tempo di esecuzione pari a 16; 8 elementi corrisponderebbero a 64 e cosi via. Ribadisco: per un set di dati irrisorio, un algoritmo di complessità quadratica, potrebbe andare bene, ma con un milione di dati, l’algoritmo potrebbe anche impiegare alcune ore per fare il suo lavoro.

Esistono molti algoritmi semplici come il bubblesort o l’insertion sort che tilizzano O(n²), non sono proprio ideali da usare ma sono i più semplici da implementare. Il motivo della loro lentezza è presto detto: al loro interno hanno un doppio ciclo for, cioè uno dentro l’altro. Esistono tantissimi esempi reali per cui non si può prescindere dall’uso di un doppio ciclo, ad esempio, l’attraversamento di una matrice (una array bidimensionale), che richiede la scansione obbligatoria delle colonne per ogni singola riga.

O(log N)

O(Log N) è la complessità logaritmica (dove il logaritmo è in base 2) che è praticamente l’opposto di o(n²), è la notazione migliore che si possa avere, se escludiamo ovviamente la notazione costante, che viene appunto ignorata durante il calcolo della complessità dell’algoritmo. In questo caso il tempo di esecuzione dell’algoritmo è proporzionale al logaritmo della dimensione dell’input. Negli algoritmi di questo tipo, ad ogni iterazione, la dimensione dell’input decresce di un fattore multiplo costante. L’esempio classico è l’algoritmo di ricerca binaria, che essenzialmente è un algoritmo divide et impera.

Ad esempio, supponiamo di avere un array ordinato di 10 elementi e di voler trovare il numero 7.

1 2 3 4 5 6 7 8 9 10

L’algoritmo divide et impera divide a metà l’array e usa il numero centrale come pivot. Quindi avremo due sottoarray:

1 2 3 4 

6 7 8 9 10

Poichè 7 è maggiore di 5, allora l’algorimo utilizzerà la seconda metà dell’array e continuerà le iterazioni dividendo a sua volta il sottoarray in altri due array, quindi, il pivot diventerà 8 (che è comunque diverso da 7) e i due array saranno:

6 7

9 10

Poichè 8 è maggiore di 7, in questo caso verrà selezionato la prima metà dell’array e si continuerà con un’ulteriore iterazione suddividendo 6 7 in due array, impostando il pivot uguale a 6

6

7

Poichè il pivot 6 è minore di 7, allora verrà selezionato l’array composto da 7, che essendo formato da un unico elemento, la funzione termina ritornando appunto il valore desiderato.

Post collegati:

Tag: